第
1题: 阅读下列说明和图,回答问题1至问题4,将解答填入答题纸的对应栏内。
【说明】
某大学欲开发一个基于Web的课程注册系统。该系统的主要功能如下:
1、验证输入信息
(1)检查学生信息:检查学生输入的所有注册所需信息。如果信息不合法,返回学生信息不合法提示;如果合法,输出合法学生信息。
(2)检查学位考试信息:检查学生提供的学位考试结果。如果不合法,返回学位考试结果不合法提示;如果合法,检查该学生注册资格。
(3)检查学生资格:根据合法学生信息和合法学位考试结果,检查该学生对欲选课程的注册资格。如果无资格,返回无注册资格提示;如果有注册资格,则输出注册学生信息(包含选课学生标识)和欲注册课程信息。
2、处理注册申请
(1)存储注册信息:将注册学生信息记录在学生库。
(2)存储所注册课程:将选课学生标识与欲注册课程进行关联,然后存入课程库。
(3)发送注册通知:从学生库中读取注册学生信息,从课程库中读取所注册课程信息,给学生发送接受提示;给教务人员发送所注册课程信息和已注册学生信息。
现采用结构化方法对课程注册系统进行分析和设计,获得如图1-1所示的0层数据流图和图1-2所示的1层数据流图。
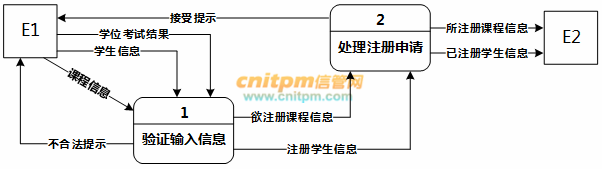
图1-1 0层数据流图
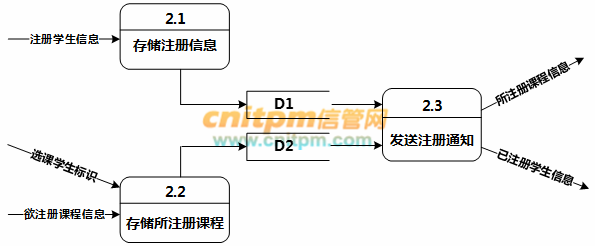
图1-2 1层数据流图
【问题1】(2分)
使用说明中的词语,给出图1-1中的实体E1和E2的名称。
【问题2】(2分)
使用说明中的词语,给出图1-2中的数据存储D1和D2的名称。
【问题3】(8分)
根据说明和图中术语,补充图1-2中缺失的数据流及其起点和终点。
【问题4】(3分)
根据补充完整的图1-1和图1-2,说明上层的哪些数据流是由下层的哪些数据流组合而成。
答案解析与讨论:
www.cnitpm.com/st/3813320302.html第
2题: 阅读下列说明,回答问题1至问题3,将解答填入答题纸的对应栏内。
【说明】
某快递公司为了方便管理公司物品运送的各项业务活动,需要构建一个物品运送信息管理系统。
【需求分析结果】
(1)快递公司有多个分公司,分公司信息包括分公司编号、名称、经理、办公电话和地址。每个分公司可以有多名员工处理分公司的日常业务,每位员工只能在一个分公司工作。每个分公司由一名经理负责管理分公司的业务和员工,系统需要记录每个经理的任职时间。
(2)员工信息包括员工号、姓名、岗位、薪资、手机号和家庭地址。其中,员工号唯一标识员工信息的每一个元组。岗位包括经理、调度员、业务员等。业务员根据客户提交的快件申请单进行快件受理事宜,一个业务员可以受理多个客户的快件申请,一个快件申请只能由一个业务员受理。调度员根据已受理的申请单安排快件的承运事宜,例如:执行承运的业务员、运达时间等。一个业务员可以执行调度员安排的多个快件的承运业务。
(3)客户信息包括客户号、单位名称、通信地址、所属省份、联系人、联系电话、银行账号。其中,客户号唯一标识客户信息的每一个元组。当客户要寄快件时,先要提交快件申请单,申请号由系统自动生成。快件申请信息包括申请号、客户号、发件人、发件人电话、快件名称、运费、发出地、收件人、收件人电话、收件地址。其中,一个申请号对应唯一的一个快件申请,一个客户可以提交多个快件申请,但一个快件申请由唯一的一个客户提交。
【概念模型设计】
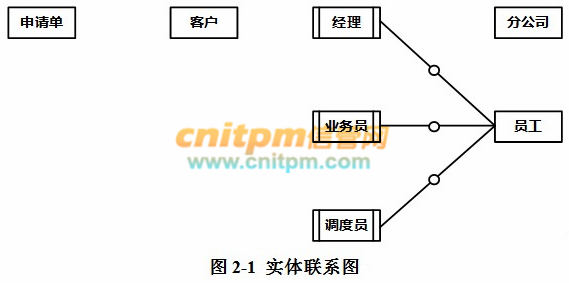
根据需求阶段收集的信息,设计的实体联系图(图2-1)和关系模型(不完整)如下:
【关系模型设计】
分公司(分公司编号,名称,经理,办公电话,地址)
员工(员工号,姓名, (a) ,岗位,薪资,手机号,家庭地址)
客户(客户号,单位名称,通信地址,所属省份,联系人,联系电话,银行账号)
申请单( (b) ,发件人,发件人电话,发件人地址,快件名称,运费,收件人,收件人电话,收件地址,受理标志,业务员)
安排承运( (c) ,实际完成时间,调度员)
【问题1】
根据问题描述,补充五个联系,完善图2-1的实体联系图。联系名可用联系1、联系2、联系3、联系4和联系5代替,联系的类型分为1:1、1:n和m:n(或1:1、1:*和*:*)。
【问题2】
(1)根据实体联系图,将关系模式中的空(a)~(c)补充完整;
(2)给出员工、申请单和安排承运关系模式的主键和外键。
【问题3】
(1)客户关系的通信地址可以进一步分为邮编、省、市、街道,那么该属性是否属于简单属性,为什么?请用100字以内的文字说明。
(2)假设分公司需要增设一位经理的职位,那么分公司与经理之间的联系类型应修改为(d),分公司的主键应修改为(e)。
答案解析与讨论:
www.cnitpm.com/st/38134841.html第
3题: 阅读下列说明和图,回答问题1至问题3,将解答填入答题纸的对应栏内。
【说明】
某航空公司会员积分系统(CFrequentFlyer)的主要功能描述如下:
乘客只要办理该航空公司的会员卡,即可成为普卡会员(CBasic)。随着飞行里程数的积累,可以从普卡会员升级到银卡会员(CSilver)或金卡会员(CGold)。非会员(CNonMember)不能积累里程数。
每年年末,系统根据会员在本年度累积的里程数对下一年会员等级进行调整。
普卡会员在一年内累积的里程数若满25000英里但不足50000英里,则自动升级为银卡会员;若累积的里程数在50000英里以上,则自动升级为金卡会员。银卡会员在一年内累积的里程数若在50000英里以上,则自动升级为金卡会员。
若一年内没有达到对应级别要求的里程数,则自动降低会员等级。金卡会员一年内累积的里程数若不足25000英里,则自动降级为普卡会员;若累积的里程数达到25000英里,但是不足50000英里,则自动降级为银卡会员。银卡会员一年内累积的里程数若不足25000英里,则自动降级为普卡会员。
采用面向对象方法对会员积分系统进行分析与设计,得到如图3-1所示的状态图和图3-2所示的类图。
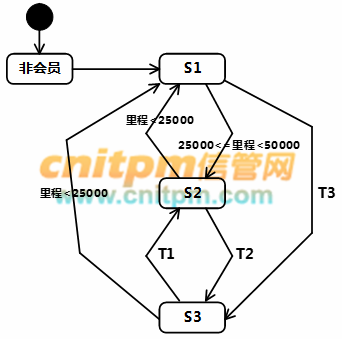
图3-1 状态图
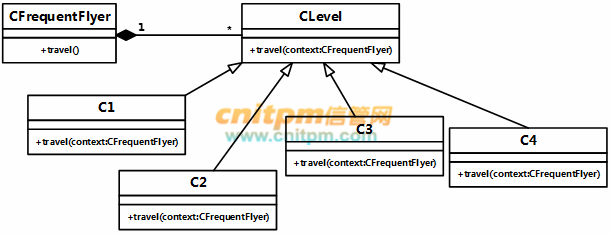
图3-2 的类图
【问题1】(6分)
根据说明中的描述,给出图3-1中S1~S3处所对应的状态以及T1~T3处所对应的迁移的名称。
【问题2】(4分)
根据说明中的描述,给出图3-2中C1~C4所对应的类名(类名使用说明中给出的英文词汇)。
【问题3】(5分)
图3-2所示的类图中使用了哪种设计模式?在这种设计模式下,类CFrequentFlyer必须具有的属性是什么?C1~C4中的travel方法应具有什么功能?
答案解析与讨论:
www.cnitpm.com/st/3813521296.html第
5题: 阅读下列说明和C++代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
欲开发一个绘图软件,要求使用不同的绘图程序绘制不同的图形。以绘制直线和圆形为例,对应的绘图程序如表5-1所示。

该绘图软件的扩展性要求,将不断扩充新的图形和新的绘图程序。为了避免出现类爆炸的情况,现采用桥接(Bridge)模式来实现上述要求,得到如图5-1所示的类图。
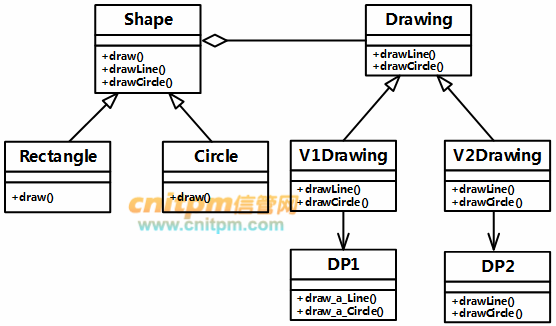
图5-1 类图
【C++代码】
class DP1{
public:
static void draw_a_line(double x1,double y1,double x2,double y2){/*代码省略*/}
static void draw_a_circle(double x,double y,double r){ /*代码省略*/}
};
class DP2{
public:
static void drawline(double x1,double x2,double y1,double y2){/*代码省略*/}
static void drawcircle(double x,double y,double r){/*代码省略*/}
};
class Drawing{
public:
(1) ;
(2) ;
};
class V1Drawing:public Drawing{
public:
void drawLine(double x1,double y1,double x2, double y2){/*代码省略*/}
void drawCircle(double x, double y, double r){ (3) ;}
};
class V2Drawing:public Drawing{
public:
void drawLine(double x1,double y1,double x2, double y2){/*代码省略*/}
void drawCircle(double x, double y, double r){ (4) ;}
};
class Shape{
public:
(5) ;
Shape(Drawing * dp){ _dp = dp;}
void drawLine(double x1, double y1,double x2, double y2){_dp->drawLine(x1,y1,x2,y2);}
void drawCircle(double x, double y, double r){_dp->drawCircle(x,y,r);}
private: Drawing * _dp;
};
class Rectangle:public Shape{
public:
void draw(){/*代码省略*/}
//其余代码省略
};
class Circle:public Shape{
private: double _x,_y,_r;
public:
Circle(Drawing * dp, double x, double y, double r): (6) {_x = x; _y = y; _r = r;}
void draw(){ drawCircle(_x, _y, _r);}
};
答案解析与讨论:
www.cnitpm.com/st/3813723129.html第
6题: 阅读下列说明和Java代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
欲开发一个绘图软件,要求使用不同的绘图程序绘制不同的图形。以绘制直线和圆形为例,对应的绘图程序如表6-1所示。

该绘图软件的扩展性要求,将不断扩充新的图形和新的绘图程序。为了避免出现类爆炸的情况,现采用桥接(Bridge)模式来实现上述要求,得到如图6-1所示的类图。
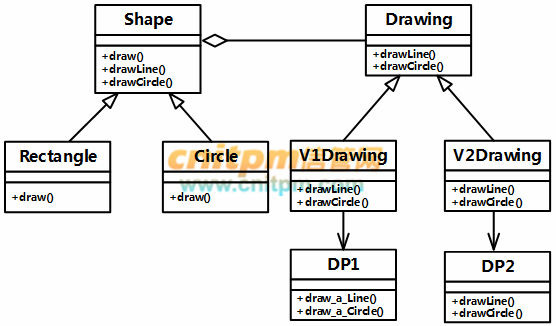
图6-1 类图
【Java代码】
(1) Drawing{
(2) ;
(3) ;
}
class DP1{
static public void draw_a_line(double x1, double y1, double x2, double y2) {/*代码省略*/}
static public void draw_a_circle(double x, double y, double r) {/*代码省略*/}
}
class DP2{
static public void drawline(double x1, double y1, double x2 ,double y2){/*代码省略*/}
static public void drawcircle (double x, double y, double r){/*代码省略*/}
}
class V1Drawing implements Drawing{
public void drawLine(double x1, double y1, double x2 ,double y2){/*代码省略*/}
public void drawCircle(double x, double y, double r){ (4) ;}
}
class V2Drawing implements Drawing{
public void drawLine(double x1, double y1, double x2 ,double y2){/*代码省略*/}
public void drawCircle (double x, double y, double r){ (5) ;}
}
abstract class Shape{
private Drawing _dp;
(6) ;
Shape(Drawing dp) {_dp=dp;}
public void drawLine(double x1, double y1, double x2 ,double y2){_dp.drawLine(x1,y1,x2,y2); }
public void drawCircle (double x, double y, double r){ _dp.drawCircle(x,y,r);}
}
class Rectangle extends Shape{
private double _x1,_x2,_y1,_y2;
public Rectangle(Drawing dp,double x1, double y1, double x2 ,double y2) {/*代码省略*/}
public void draw(){/*代码省略*/}
}
class Circle extends Shape{
private double _x, _y, _r;
public Circle(Drawing dp,double x, double y, double r) {/*代码省略*/}
public void draw(){drawCircle(_x,_y,_r);}
}
答案解析与讨论:
www.cnitpm.com/st/3813815424.html









